Sound Waves

Sound Waves and Acoustics

Sound waves are a fundamental part of our daily experience. They are responsible for the sounds we hear and play a crucial role in various fields, including music, engineering, and medicine. Let's explore some key concepts related to sound waves and acoustics.

What Is a Wave?

A wave is a disturbance that propagates through space or a medium, transporting energy without transporting matter. It can be described by various characteristics:

• Amplitude (A): The maximum displacement of particles in the medium from their rest position. It determines the loudness or intensity of the sound.

• Wavelength (λ): The distance between two consecutive points (e.g., crests or troughs) in a wave. It is inversely proportional to the frequency.

• Frequency (f): The number of complete cycles (oscillations) of a wave per unit of time, usually measured in Hertz (Hz). Higher frequencies result in higher-pitched sounds.

• Wave Speed (v): The speed at which the wave propagates through the medium. It's related to frequency and wavelength as v = fλ.

Sound Waves

Sound waves are a type of mechanical wave that travels through a medium, such as air, water, or solids. They consist of compressions and rarefactions of the medium, leading to variations in pressure.

• Speed of Sound: The speed of sound varies with the medium. In dry air at room temperature, it's approximately 343 meters per second (m/s).

Characteristics of Sound

Sound waves produce various perceptual qualities that we associate with the sounds we hear:

• Frequency (Pitch): The frequency of a sound wave determines its pitch. Higher frequencies correspond to higher-pitched sounds, while lower frequencies result in lower-pitched sounds. Pitch is measured in Hertz (Hz).

• Amplitude (Loudness): The amplitude of a sound wave affects its loudness. Greater amplitudes produce louder sounds.

• Timbre (Tone Quality): Timbre is the unique quality or color of a sound that distinguishes it from other sounds, even when they have the same pitch and loudness.

Intensity and Sound Level

• Intensity (I): Intensity measures the amount of energy transmitted by a sound wave per unit of time and unit area. It is related to the square of the amplitude and inversely proportional to the square of the distance from the source.

• Sound Level (L or LdB): Sound level quantifies the intensity of a sound wave in logarithmic units called decibels (dB). The formula is L = 10 * log10(I / I0), where I0 is the reference intensity (usually the quietest sound the average human ear can detect).

Intensity of Sound Waves

Sound intensity (I) measures the amount of energy carried by a sound wave per unit of time and unit area. It quantifies how "loud" a sound is and is typically measured in watts per square meter (W/m²).

The formula to calculate sound intensity is:

I=A/P​

Where:

• I is the sound intensity in watts per square meter (W/m²).
• P is the power of the sound wave in watts (W).
• A is the cross-sectional area through which the sound wave is passing in square meters (m²).

To calculate sound intensity, you need to know the power of the sound source and the area over which the sound wave is spreading.

For example, if a loudspeaker emits sound with a power output of 10 watts, and this sound wave spreads uniformly over an area of 5 square meters, you can calculate the intensity as follows:

I=10W/5 m²=2W/m2

So, the intensity of the sound at that particular location is 2 watts per square meter (W/m²).

Understanding sound intensity is crucial in various applications, such as noise control, audio engineering, and assessing the impact of sound on the human ear.

Decomposition of a Sound Wave

Sound waves can often be described as a combination of multiple sine waves, each with different frequencies, amplitudes, and phases. This decomposition is based on the principles of Fourier analysis and helps us understand the complex nature of sounds. There are two key components in the decomposition of a sound wave:

1. Fundamental Frequency (Fundamental): The fundamental frequency is the lowest frequency component of a sound wave. It determines the pitch or musical note of the sound. For example, when you pluck a guitar string, the fundamental frequency corresponds to the note you hear. In mathematical terms, it's the frequency at which the sound wave repeats itself over time.

2. Harmonics: Harmonics are integer multiples of the fundamental frequency. They represent higher-pitched components present in the sound wave. The presence and amplitudes of harmonics contribute to the timbre or tone color of the sound. For example, the overtones produced by a musical instrument create its unique timbre.

The process of decomposing a complex sound wave into its fundamental and harmonic frequencies is called spectral analysis. It involves identifying the various sine waves that, when added together, recreate the original sound wave.

For example, if you record the sound of a musical instrument, a Fourier analysis might reveal that the fundamental frequency corresponds to the note being played, while the harmonics contribute to the instrument's characteristic sound.

Understanding the decomposition of sound waves is essential in music, audio engineering, and speech processing, as it allows us to manipulate and recreate different sounds.

Célérité onde progressive

V=(Xb-Xa/Tb-Ta)

• V(m.s-1)
• X(m)
• T(s)

Onde mécanique périodique

λ=V * T = V/f

• λ(m)
• V(m.s-1)
• T(s)
• f(Hz)

Remarks:

• Sound Level Measurement: The intensity of sound is often measured in decibels (dB). Devices such as sound level meters or decibel meters are used to measure the sound level. These devices quantify the intensity or loudness of a sound, providing valuable information in fields like noise pollution monitoring and audio engineering.

• Audible Frequency Range: The typical range of frequencies that the human ear can perceive is approximately 20 Hz to 20,000 Hz (20 kHz). Frequencies below this range are considered infrasound and are often generated by natural phenomena like earthquakes. Frequencies above this range are termed ultrasound and are used in medical imaging, cleaning processes, and pest control, among other applications.

• 

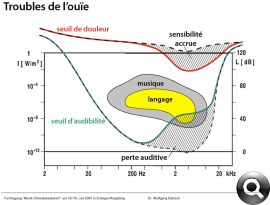
Understanding sound waves and acoustics is essential in fields like music, engineering (e.g., designing audio systems), and medicine (e.g., medical imaging). It allows us to create, analyze, and manipulate sound to enrich our lives and improve various technologies.